torch.tensor(data, requires_grad=False)
data: 保持するデータ(配列っぽいものならなんでも)- リスト、タプル、NumPy配列、スカラ、...
requires_grad: 勾配(gradient)を保持するかどうかのフラグ- デフォルトはFalse
- 勾配の計算(自動微分)を行う場合はTrueにする
>>> x = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]], requires_grad=True)
[[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]]という行列を保持するTensor型のオブジェクトを作成
(数 を定義)
(requires_grad=Trueとすれば、勾配計算が可能なTensor型を作成できる)
これらを勾配計算が可能なTensor型として表現してください。
(このページの内容は、実際にやらなくてもやり方がわかればOKです)
↓ 問題の続き次のページへ
(実際にやってください)
- 整数 を勾配計算が可能なTensor型として表現することを試みてください。また、その結果を確認して説明できるようにしてください。
- 1から100までの値を並べた10x10行列、つまり
を勾配計算が可能なTensor型として表現してください。(次ページヒント)
1, 2, 3: 講義資料を遡って、torch.tensorの第一引数と作成されるTensor型の対応を見比べてみましょう。
4: Pythonのエラーは、
~~たくさん書いてある~
~~Error: {ここにエラーの概要}
という形式です。"~~Error"というところのすぐ後に書いてある概要を確認してみましょう。
5: 3が解けたのであれば、torch.tensorの第一引数にどのようなオブジェクトをが来るべきかはわかるはずです。あとはそのリストの構築方法を考えましょう。
1~3.
# 1
x = torch.tensor(3.0, requires_grad=True)
# 2
x = torch.tensor([3.0, 4.0, 5.0], requires_grad=True)
# 3
x = torch.tensor([[3.0, 4.0, 5.0], [6.0, 7.0, 8.0]], requires_grad=True)
次のページへ
x = torch.tensor(3, requires_grad=True)
と入力してみると、
"RuntimeError: Only Tensors of floating point and complex dtype can require gradients"となります。これは、勾配が計算可能なのは浮動小数点数と複素数のみであるということを意味しています。
次のページへ
- (解答例) 一番素直なやつ
>>> matrix = []
>>> for i in range(10):
... row = []
... for j in range(10 * i + 1, 10 * i + 11):
... row.append(float(j))
... matrix.append(row)
...
>>> torch.tensor(matrix, requires_grad=True)
- (解答例2) 一番素直なやつ 内包表記ver
>>> x = torch.tensor([[float(i) for i in range(10 * j + 1, 10 * j + 11)] for j in range(10)]
他にも別解はたくさんありますが、書き方に関わらず作れればここまでの内容は理解できているので
)
Tensor型は、「数」なので当然各種演算が可能
x = torch.tensor(2.0, requires_grad=True)
- 四則演算
x + 2
# -> tensor(4., grad_fn=<AddBackward0>)
x * 2
# -> tensor(4., grad_fn=<MulBackward0>)
各種 数学的な(?) 関数も利用可能
torch.sqrt(x)
# -> tensor(1.4142, grad_fn=<SqrtBackward0>)
torch.sin(x)
# -> tensor(0.9093, grad_fn=<SinBackward0>)
torch.exp(x)
# -> tensor(7.3891, grad_fn=<ExpBackward0>)
ここまでの内容は別にPyTorchを使わなくてもできること
PyTorchは、計算と共に勾配の計算ができる!

requires_grad=TrueであるTensor型に対して計算を行うと、行われた演算が記録されたTensorができる.
x = torch.tensor(2.0, requires_grad=True)
足し算をする。
y = x + 2
⬇︎
print(y)
これの出力は、
tensor(4., grad_fn=<AddBackward0>)
⇨ Addという演算がyに記録されている!
普通のPythonの数値では、
x = 2
y = x + 2
print(y) # -> 4.0
yがどこから来たのかはわからない(値としてを持っているだけ)
 PyTorchは、
PyTorchは、backward関数をつかって記録された演算を辿ることで、勾配を計算できる
x = torch.tensor(2.0, requires_grad=True)
y = x + 2
⬇︎
y.backward()
⬇︎
print(x.grad) # -> tensor(1.)
- 変数(Tensor型)の定義
- 計算
- backward()
# 1. 変数(Tensor型)の定義
x = torch.tensor(2.0, requires_grad=True)
# 2. 計算
y = x + 2
# 3. backward()
y.backward()
すると、x.gradに計算された勾配が格納される。
なぜこんな設計なのか気になった人は、講義が終わったら資料末の「発展的話題: 自動微分のアルゴリズム」を読んでみてください。現段階では、今回はこのセットで計算できる!ということを覚えてもらえればokです。
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward() 定義→計算→backw
例1) の微分
x = torch.tensor(2.0, requires_grad=True)
y = y = torch.sin((x + 2) + (1 + torch.exp(x ** 2)))
y.backward()
print(x.grad()) # -> tensor(-218.4625)
例2) の微分()
x = torch.tensor(2.0, requires_grad=True)
y = x ** 2
z = 2 * y + 3
z.backward()
print(x.grad) # -> tensor(8.) ... backward()した変数に対する勾配!(この場合はz)
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = 2 * x[0] + 3 * x[1] + 4 * x[2]
y.backward()
print(x.grad) # -> tensor([2., 3., 4.])
と対応
A = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]], requires_grad=True)
y = torch.sum(A)
y.backward()
print(A.grad) # -> tensor([[1., 1., 1.],
# [1., 1., 1.]])
と対応
x = torch.tensor(2.0, requires_grad=True)
y = torch.tensor(3.0, requires_grad=True)
z = 2 * x + 4 * y
z.backward()
print(x.grad) # -> tensor(2.)
print(y.grad) # -> tensor(4.)
に対応
x = torch.tensor(2.0, requires_grad=True)
def f(x):
return x + 3
def g(x):
return torch.sin(x) + torch.cos(x ** 2)
if rand() < 0.5:
y = f(x)
else:
y = g(x)

(if文があるから, for文があるから, 自分が定義した関数に渡したから...ということは関係なく、実際に適用される演算のみが問題になる)
抑えてほしいポイント
- 任意の(勾配が定義できる)計算をTensor型に対して適用すれば、常に自動微分可能
- 定義→計算→backward() の流れ
- ベクトル、行列など任意のTensor型について微分可能。多変数関数の場合も同様
- 「実際に適用される演算」さえ微分可能ならOK
-
のにおける微分係数をPyTorchを使って求めよ。
-
の
における勾配をPyTorchを使って求めよ。 -
, , に対して、の勾配をPyTorchを使って求めよ。なお、行列積は
torch.matmul関数で利用できる。
(次ページヒント)
x = torch.tensor(3.0, requires_grad=True)
y = x ** 2 + 2 * x + 1
y.backward()
print(x.grad) # -> tensor(8.)
x = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = x[0] ** 2 + x[1] ** 2 + x[2] ** 2
y.backward()
print(x.grad) # -> tensor([2., 4., 6.])
W = torch.tensor([[1.0, 2.0, 3.0], [4.0, 5.0, 6.0]], requires_grad=True)
x1 = torch.tensor([[1.0, 2.0]], requires_grad=True)
x2 = torch.tensor([1.0, 2.0, 3.0], requires_grad=True)
y = torch.matmul(torch.matmul(x1, W), x2)
y.backward()
print(W.grad)
print(x1.grad)
print(x2.grad)
の勾配降下法による最小値の探索
from math import exp
x = 3
lr = 0.0005
# xでの微分係数
def grad(x):
return 2 * x - exp(-x)
for i in range(10001):
# 更新式
x = x - lr * grad(x)
if i % 1000 == 0:
print('x_', i, '=', x)
これまでは、導関数gradを我々が計算しなければいけなかった
⇨自動微分で置き換えられる!
import torch
x = torch.tensor(3.0, requires_grad=True)
def f(x):
return x ** 2 + torch.exp(-x)
for i in range(10001):
y = f(x)
y.backward()
x = x - lr * x.grad
実際に動かすにあたっては軽微な修正が必要ですが、スペースが足りないのでここには載せていません。
詳しくは配布のソースコードを参照してください。
今ならこいつを倒せるはず
最小化してください。
- 複雑な関数
の最小値を、PyTorchを用いて勾配降下法を実装することで求めてください。
実装にあたっては、配布ソースコードのPyTorchによる勾配降下法」の項を参照してください。
(次ページ次の問題)
- アイスの問題 ver2
とします。アイスの売り上げと気温の関係は、リンク先からコピーできます。それぞれのデータがとして与えられているとき、
を最小にするをPyTorchを用いて勾配降下法を実装することで求めてください。(次ページ次の問題)
- 損失関数
第一回の講義資料では次のような文章がありました。
「「悪さ」を最小化するのではなく「良さ」を最大化すれば良くない?と思った人もいるかもしれないですね。
実はそれはものすごくいい疑問で、次回以降で明らかになっていきます。
ひとまずは一旦疑問として抱えておいてください。」
これに対する答えを考えてみてください。
より具体的に、たとえば「明日は晴れかどうか予測する」、という問題に対して例えば「正解率」を最大化することを考えた場合、どのような点で困るか考えてください。
(次ページヒント)
1, 2.配布ソースコードの該当箇所を確認してよく見比べてください。
- 勾配降下法を使った学習ではパラメータによる損失(今回の場合は損失ではないですが)の微分を考えていました。つまり、パラメータが微小に変化したときに、損失がどれだけ変化するかを考えていました。今回の場合はこの値はどうなるでしょうか?
- サンプルコードを参照
- サンプルコードを参照
出力は最終的に「晴れ」or「晴れじゃない」のいずれかに割り振られる。したがって、パラメータが微小に変化したとしても、出力は変化しない。つまり、ほとんどの場合で微分係数が0になってしまう。これでは勾配降下法の枠組みで学習を進めることができない。
発展的話題
これらが気になる人向け
- そもそもどうやって微分をしているのか?
backward()関数はどういう働きをしているのか?- どうして定義→計算→backward()みたいな使い方をするのか?
めちゃx2余談です


最適化の文脈では、基本的にほしいものは「微分係数」であって
「導関数」である必要はない
人間が微分をする場合...
例) のにおける微分係数を求めろ
↓
だから、
PyTorchでは...
例) のにおける微分係数を求めろ
↓
x = torch.tensor(3.0, requires_grad=True)
y = x ** 2 + 2 * x + 1
y.backward()
x.grad # -> tensor(8.)
陽に導関数を求めておらず、直接導関数を求めている
どうやって?
コンピュータで微分を求めるアルゴリズムの分類
- 数値微分
- 数式微分・記号微分
- 自動微分
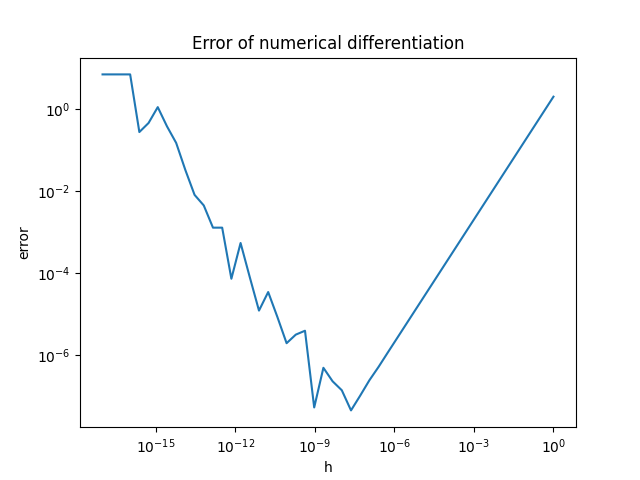
微分の定義式から直接近似する。
⬇︎ そのままPythonに
def diff(f, x, h=1e-4):
return (f(x + h) - f(x)) / h
コンピュータ上で直接極限の計算をするのは大変なので、
代わりに小さい値(上では)を使って近似する。
利点
- 実装が簡単
- (計算可能なら)どんな関数でも微分できる
欠点
- 計算量が入力変数の数に比例する
- 誤差が出やすい
- をどんどん小さくすればより高精度に計算できるわけではない(浮動小数点数の計算に伴う誤差の影響により一定以上ではむしろ悪化する)
数式微分・記号微分
演算は、計算グラフと呼ばれる有向非巡回グラフで表せる。
→
→
計算グラフに直せば、
式の操作
計算グラフの操作
計算グラフなど式を適切に表したデータ構造から
直接導関数を求める手法を数式微分や記号微分と呼ぶ。
利点
- (理論的な範囲では) 誤差が出ない
- 直接導関数を得られる
欠点
- 下手くそな実装は爆発する
- 応用領域では式は容易に非常に複雑になる。(例えば損失はデータ数の分だけ項がある総和として表されるし、尤度関数は標本の数の総積)
- 例えば積の微分では項が二つに分裂したりする。
⇨ 項の数が「大爆発」して、現実的ではなくなる
- 「プログラム」から導関数を得るのはかなりレベルの高い技術
- ニューラルネットワークなどの実装では制御構文などを含めた「普通の」プログラムも微分したくなる
- if文, for文, try/except ... ここから微分する元の関数を得るのは結構大変
自動微分
- 連鎖律(Chain rule)を利用した微分アルゴリズム
(講義資料にもあるように、自動で微分を求めるアルゴリズムの一種が「自動微分」)
連鎖律...
のこと
例) のにおける勾配
である。
(つまり、基本的な関数との合成である)
とすれば計算できる。
ここで使ったのは...
という知識
これらは、基本的な関数の微分
⇨ 基本的な関数の導関数さえ定義しておけばこれらの関数の組み合わせのどんな複雑な関数でも微分できる。
- (25)のノードに注目して。勾配を1で初期化する。
- Squareのノードに進む。
- Squareの微分は。入力は5なので、を勾配()にかける
- Addのノードに進む。
- Addの微分はどちらについても1なので、の勾配はとなる。
共通部の計算は共通化できていた。(初期化部分とSquareの微分に対応)
そして、計算は通常の計算とグラフを逆に辿る(逆伝播(back propagation))の二回で済んだ!
利点
- 計算の効率が非常に良い
- 計算回数は出力変数の数に比例する。
⇨ 機械学習は、大量のパラメータを変数として出力は損失(一つの実数)になることが多いので、圧倒的に効率がいい
- 計算回数は出力変数の数に比例する。
- PyTorchのTensor型に演算をおこなうと、「演算と同時に計算グラフが作られていく」
y.backwardを呼び出すことで、yを起点としてグラフを逆に辿り出す
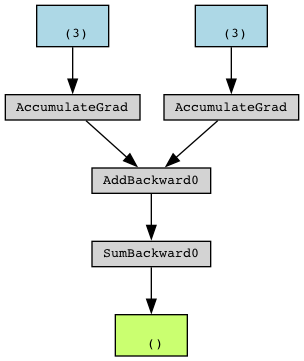
PyTorch上の計算グラフは、torchvizというライブラリを使うと可視化できる。
x = torch.tensor([1., 2., 3.], requires_grad=True)
y = torch.sin(torch.sum(x) + 2)
make_dot(y)
このように演算と同時に計算グラフを構築するスタイルをdefine-by-runと呼び、これに対して
計算グラフを先に構築してから演算を行うスタイルをdefine-and-runと呼びます。
かつては共存していましたが、今では多くのフレームワークがdefine-by-runを主要なスタイルとして採用しています。実行時に計算グラフを構築する方が圧倒的に柔軟性があるからです。
ここまでで説明したのは、グラフを出力から「逆にたどる」自動微分
⇨ 特にreverseモードの自動微分などと呼ばれる
逆に、forwardモードの自動微分と呼ばれる手法もある
二重数と呼ばれる数を使った実装が有名
⬇︎
実数の範囲内では、

ここで、新しく
なる数 を考えて、実数にこれを加えた集合の演算を考える
(虚数を考えたときと同じ展開)
そこで複素数を考えたときと全く同様に、
という形の数を考える()
このような形で表される数を二重数と呼ぶことにする
に注意すれば、
とするのが良さそう
すると、実係数多項式
に対して、
となることがわかる
やや雑ですが、微分可能ならテイラー展開することで結局実係数多項式にできるので実係数多項式の微分が正しく計算できるのであれば、微分可能な関数全てに対してうまくいきそう
https://en.wikipedia.org/wiki/Automatic_differentiation#Two_types_of_automatic_differentiationから
reverseモード同様、基本的な関数に対して二重数の演算を定義しておき、その合成として計算。
をもう一度見れば、の計算それ自体がのにおける微分係数を求める演算と対応している!
普通の関数の計算は計算グラフを入力から「順」に辿っていく
(順伝播, forward propagation) ことに他ならない
➡︎ forwardモードの自動微分
- 代表的なアプローチとして、数値微分、数式微分、自動微分があった
- 数値微分は誤差が出やすく、記号微分は柔軟な計算をしようとすると大変
- 自動微分は高速でとくにreverseモードの自動微分は機械学習において圧倒的に有用であった
もっと興味がある人は
ゼロから作るDeep Learning ❸: https://www.oreilly.co.jp/books/9784873119069/
や、
https://arxiv.org/abs/1502.05767 (自動微分全般の話)
https://arxiv.org/abs/1810.07951 (「ソースコードから微分する」話)
などを読んでみてください。
機械学習講習会 第四回
- 「ニューラルネットワークの構造」
traP アルゴリズム班 Kaggle部
2023/xx/xx
第四回: ニューラルネットワークの構造
第一回 「学習」
第二回 「勾配降下法」
第三回 「自動微分」
- 予測をするには、「モデル」を作る必要があった
- モデルのパラメータを決めるために、パラメータの関数である損失関数を導入した
- 損失関数を最小にするパラメータを求めるために勾配降下法を導入した
- 自動微分によって手で微分する必要がなくなった [← 今ココ!]
われわれができるようになったこと
データさえあれば...誤差を小さくするパラメータを
- 例え複雑な式でも
- 例え自分で導関数を見つけられなくても
求められるようになった!
(== 学習ができるようになった!)
ここまでは のかたちを仮定してきた
⇨ われわれの学習手法はこの仮定に依存しているか?
結論: 依存していない
我々の手法(自動微分と勾配降下法による学習)で満たすべき条件は、
が について微分可能である
ことのみ!
⇨ この条件を満たす関数なら文字通りどんなものでも学習できる!
今日のおはなし
損失関数
のを変えよう
は、をどんなに変えても常に直線
⇨ 直線以外の関係を表現できない
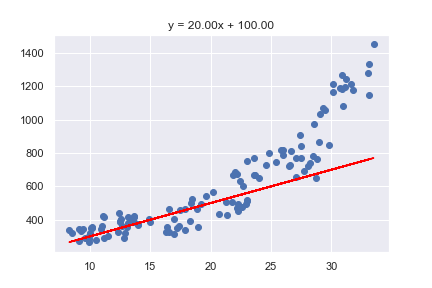
でも動く
でも動く
でも動く
⇨ 直線以外を表現することはできるが
- 二次曲線
- sin
- 指数関数
しか表現できない...
⇨ これらのパラメータどんなにいじっても
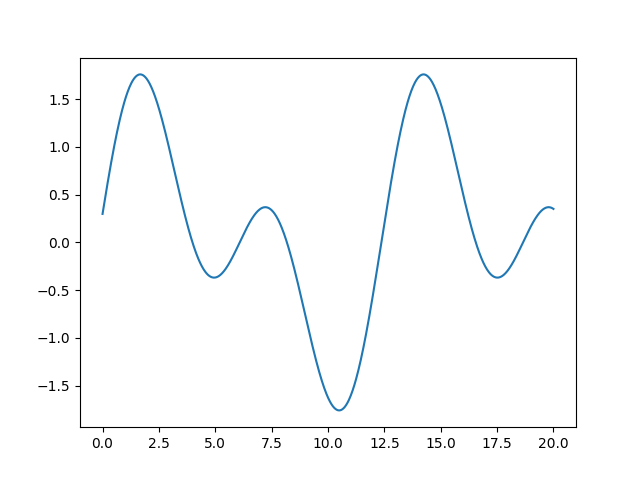
みたいなのは表現できない
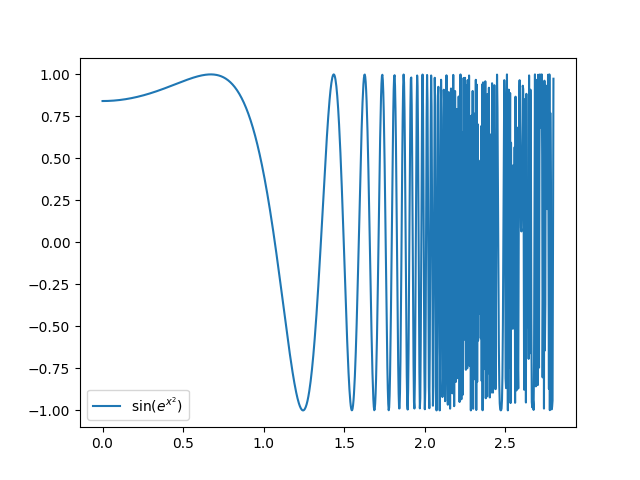
 アイデア1: 関数を合成する
アイデア1: 関数を合成する
はそれぞれ単体だと単純な関数だが、
合成してみると....?
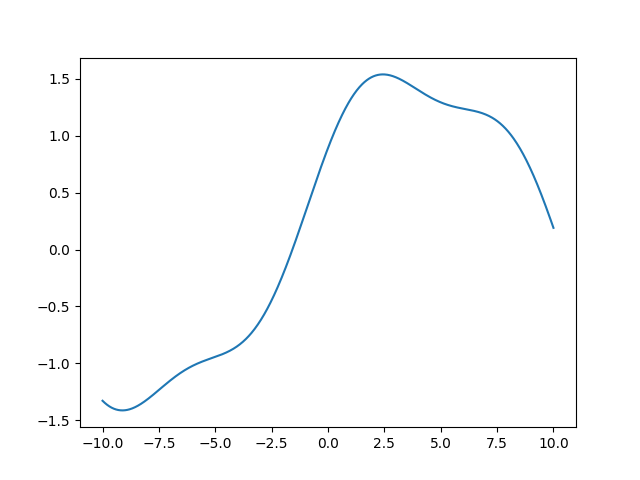
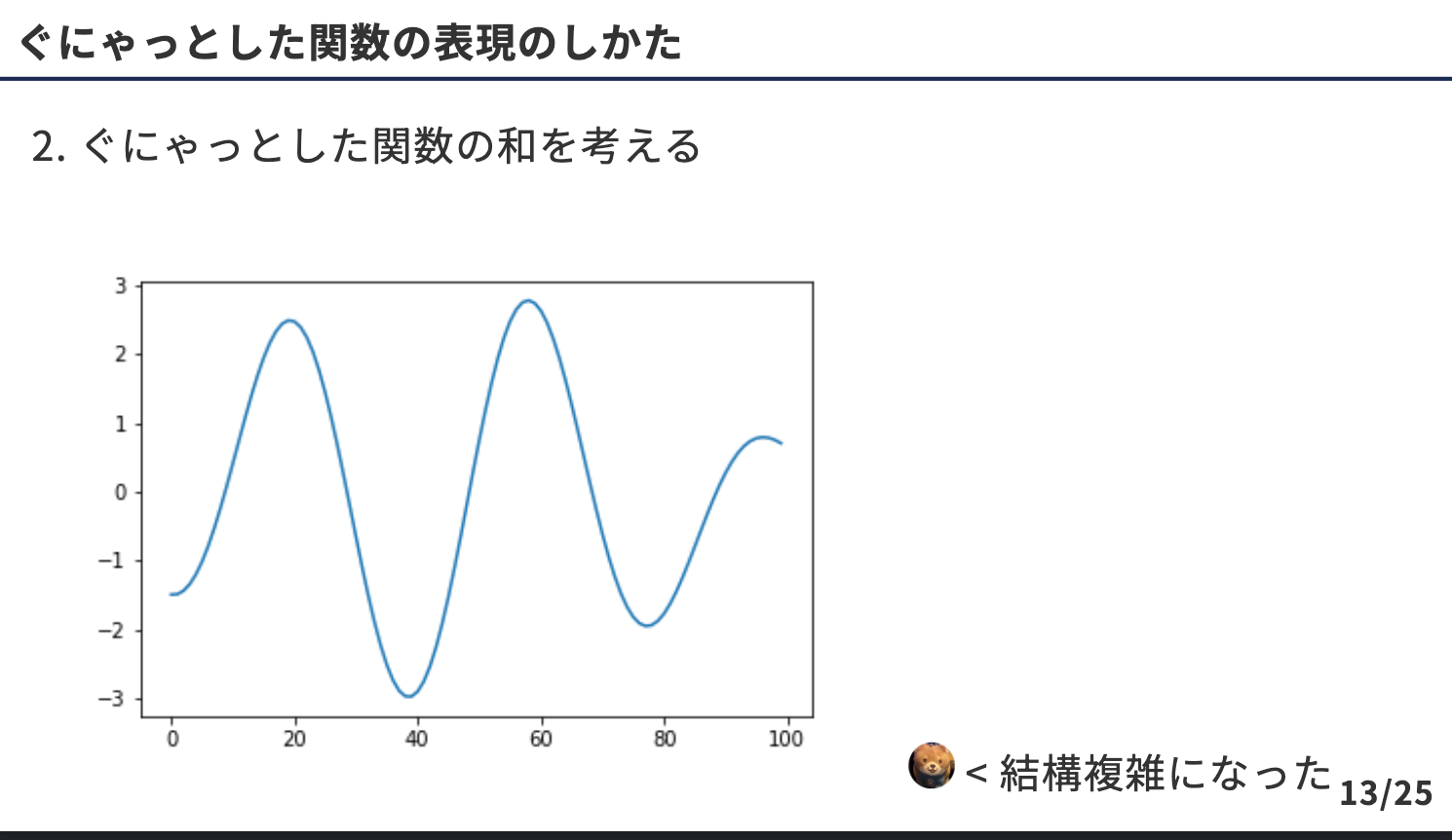
 アイデア2: 和をとる
アイデア2: 和をとる
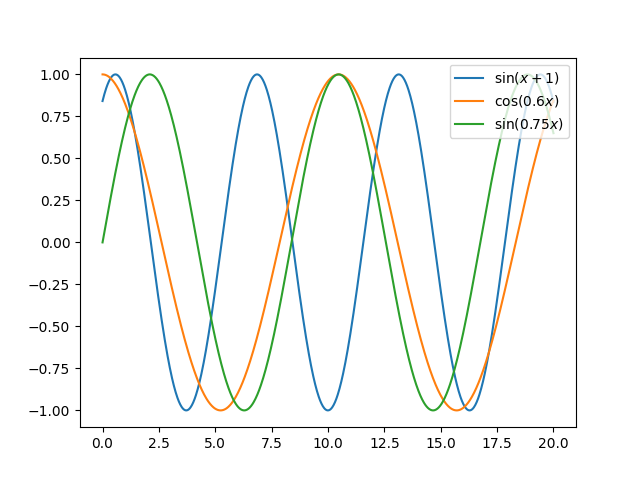
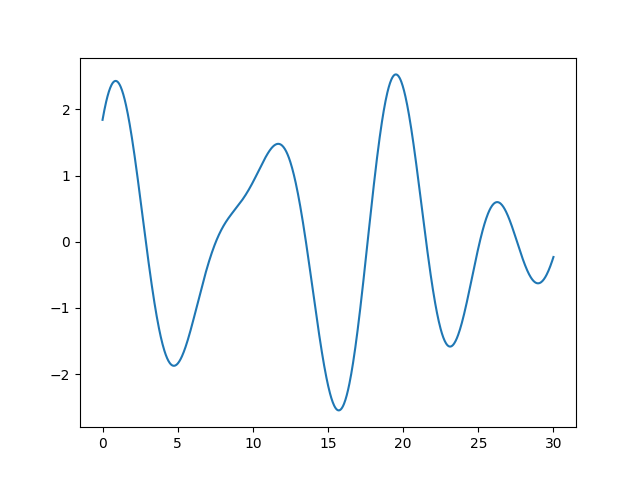
⇨ ベースにした三角関数の和をとると...
 < 実質ASMR
< 実質ASMR
 わりと簡単めの関数の
わりと簡単めの関数の
1. 合成
2. 和
を考えたら結構複雑なやつも表現できる
パラメータとして
,
,
をもつ
⇩
のとき
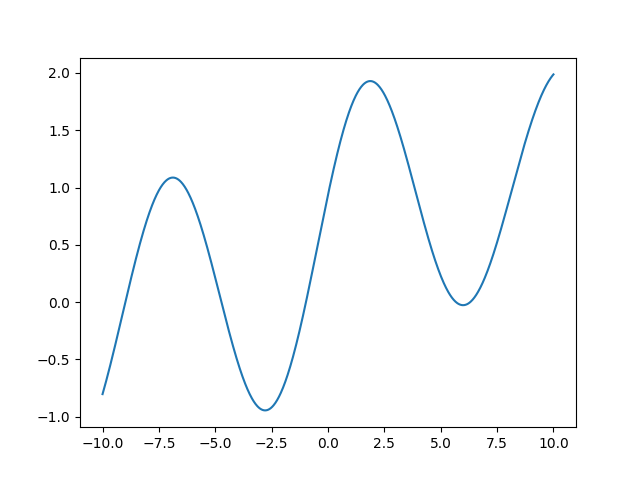
のとき
「基になる関数」にどのような関数を選ぶべきか?
- 三角関数?
- 多項式関数?
- 指数関数?
- もっと別の関数?
...
これまでの我々のアプローチを思い出すと、
「変化させるのが可能なところはパラメータにして、学習で求める」
「基になる関数」もパラメータに
よって変化するようにしよう
ニューラルネットワーク
-
最近流行りの機械学習モデルは基本的にニューラルネットワークをつかっている
-
ある程度以上複雑な問題では、たいていの場合ニューラルネットワークが最も精度が出やすい
例) 画像分類, 音声分類, 画像生成, 対話 ...

基本単位: レイヤー
ニューラルネットワークは、「レイヤー(層)」と呼ばれる関数の合成によって構成されるモデル
基本単位: レイヤー
-
入力層
入力を受け取るレイヤー -
出力層
出力を出力するレイヤー -
中間層(隠れ層, hidden layer)
それ以外のレイヤー
データの流れは、
入力層 → 中間層 → 中間層 → ... → 出力層
もっとも普遍的・基本のレイヤー
と (は適当に定めた自然数)
全結合層が固有にもつ「活性化関数」を用いて
入力としてを受け取り、
を出力する。
-
個の入力を受け取り、個出力する
-
複雑な関数を表現するアイデア...
- アイデア1. 合成
- アイデア2. 和をとる
をする
1. 個の入力を受け取り、個出力する
「 と (は適当に定めた自然数)
全結合層が固有にもつ「活性化関数」を用いて
入力としてを受け取り、
を出力する」
-
複雑な関数を表現するアイデア...
- アイデア1. 合成
- アイデア2. 和をとる
をする
非線形関数
-
シグモイド関数
-
ReLU関数
-
tanh関数
合成を繰り返す
⇨ 複雑な関数を表現
個の出力のひとつに注目してみる
⇨
は、
 とおなじことをしている
とおなじことをしている
はそれまでの層でを通した、非線形な関数
➡︎ 非線形関数の重みつき和
➡︎ 複雑な非線形関数を表現できる! + さらにそれを非線形関数に通す
演算を 回繰り返す
( 次元ベクトル → , → , → , → 次元ベクトルへと
変換されながら計算が進んでいく)
ここで、
は非常に複雑なの非線形な関数
+ これはパラメータによって変化する
「基になる関数」もパラメータに
よって変化するようにしよう
とくに、全結合層のみからなるニューラルネットワークを
多層パーセプトロン (Multi Layer Perceptron, MLP) という
⇨ ニューラルネットへ
 < どれくらい表現能力が変わったのか?
< どれくらい表現能力が変わったのか?
結論
直線 ⇨ 任意の関数
(注) 正確な表現ではありません!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
ニューラルネットワークの万能近似定理(普遍性定理)
隠れ層を一つ持つニューラルネットワークは、
任意の連続関数を表現できる
今回の講習会できちんとこの辺を論じると第300回までいくこと間違いなしなのでかなりアバウトな話になっていますので、きちんと議論がしたくて興味がある人は (https://qiita.com/mochimochidog/items/ca04bf3df7071041561a) などに詳しくまとまっているので、読んでみてください。
-
我々の学習手法は、というモデルの構造自体に直接依存しているわけではなかった
-
そして、というモデルの構造では直線しか表現することができないので、違う形を考えることにした
-
「基になる」簡単な関数の、合成と和を考えることでかなり複雑な関数も表現できることがわかった
-
「基になる」関数の選び方を考える上で、この関数自体もパラメータによって変化させるモデルとして、ニューラルネットワークを導入した
-
ニューラルネットワークは任意の関数を表現できることがわかった
第5回 ニューラルネットワークの学習と評価
- He, Xavierの初期化
- 確率的勾配降下法
- 損失関数
- オプティマイザ
- バリデーションと性能評価
- ハイパーパラメータ
Next ⇨ 第6回 ニューラルネットワークの実装
- ニューラルネットワークがなんでも表現できるぜ!!という主張は、
条件を変えていろいろある - ここでは一番有名(たぶん)なもの[1]について直感的な証明をする
[1]https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.441.7873&rep=rep1&type=pdf
を満たす関数を「シグモイド型関数」と呼ぶことにし、
として、 を 上の連続関数の集合とする。
[シグモイド型関数の重ね合わせによる近似]
「任意の に対して、ある と が存在して、
が
を満たす。
について、はシグモイド型関数
⇨ をバカみたいに大きくするとどうなる?
は
とすると、がちょっともで正ならば, そうでなければになる。
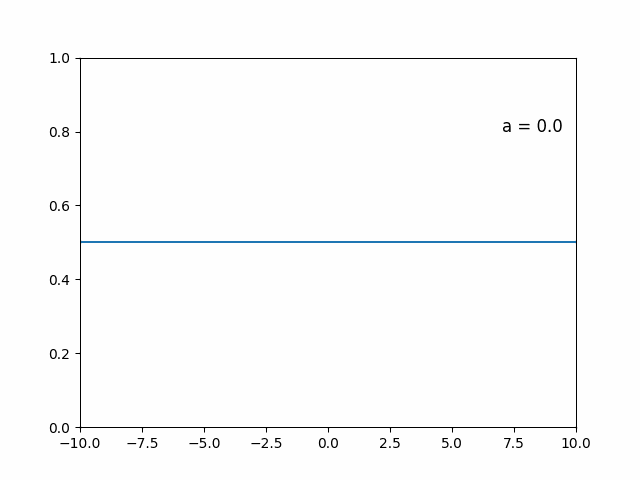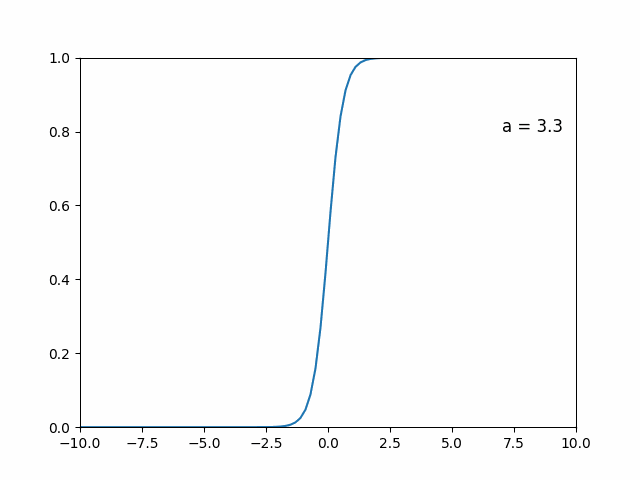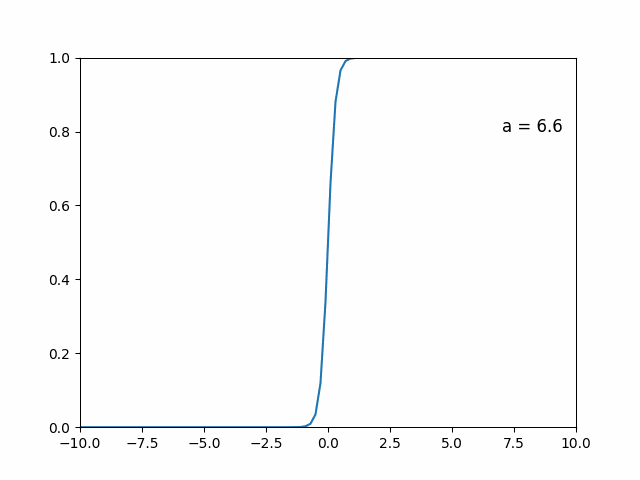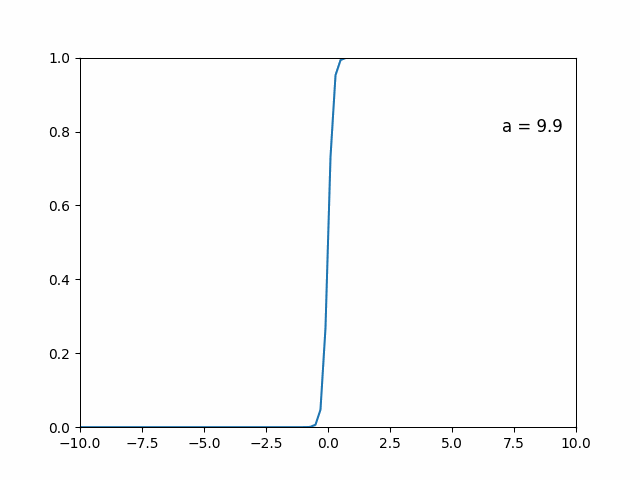
「直感的な」証明です(大声)
は
とすると、 がちょっともで正ならば, そうでなければになる。
⇨ を適当に調整すれば、狙った点で、
とすることができる. (例: なら )
を負のデカ数にすると、逆verもできる。
すると、
について、正の大きな数によってステップ関数にしたものと
負の大きな数によってステップ関数にしたものを足し合わせることで、
矩形関数を作ることができる。
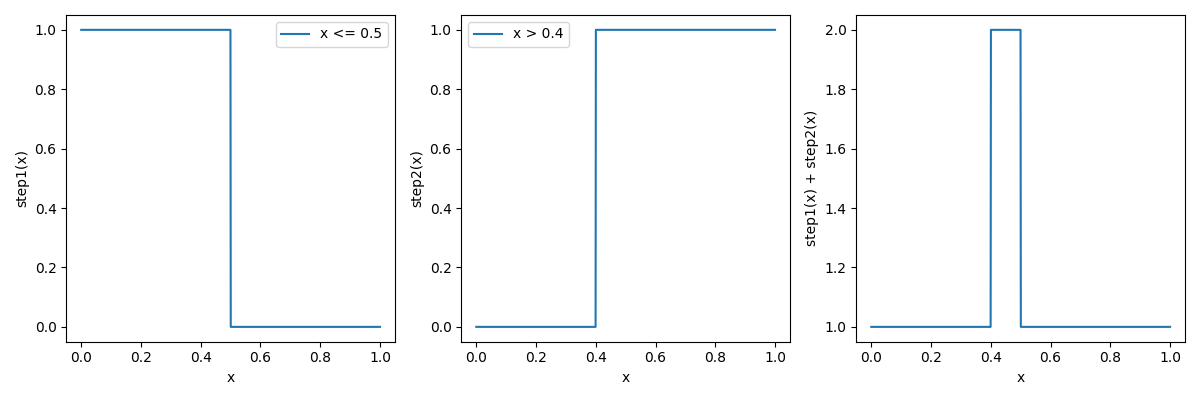

連続関数を全てこれの和としてみればよい
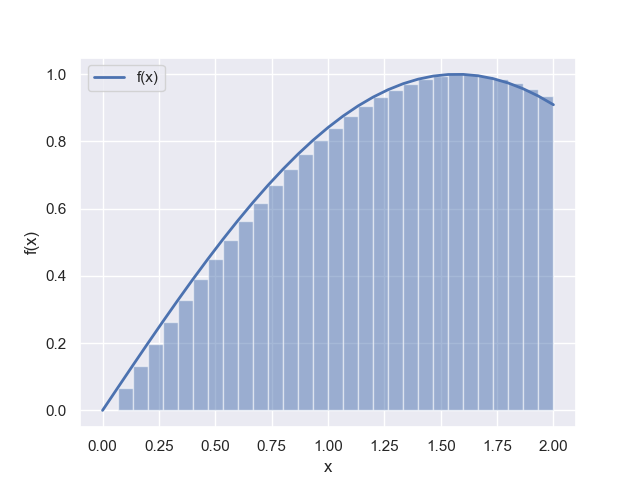
任意の連続関数を近似できるのはニューラルネットワークだけ?
⇨ NO

+ あくまでそのようなが存在するという主張であって、
それを求める方法については何ら保証していない
⇨ ニューラルネットワークの優位性を考えるなら、もうちょい議論を進めていく必要がある
(例えば今回は連続関数だけを考えたが実際に得たい関数は常にそうか?の得やすさはどうか?)
機械学習講習会 第五回
- 「ニューラルネットワークの学習と評価」
traP アルゴリズム班 Kaggle部
2023/6/28
第五回: ニューラルネットワークの
学習と評価
 「ニューラルネットワーク」を導入して、
「ニューラルネットワーク」を導入して、
任意の関数を表現できるようになった!
-
我々の学習手法は、というモデルの構造自体に直接依存しているわけではなかった
-
そして、というモデルの構造では直線しか表現することができないので、違う形を考えることにした
-
「基になる」簡単な関数の、合成と和を考えることでかなり複雑な関数も表現できることがわかった
-
「基になる」関数の選び方を考える上で、この関数自体もパラメータによって変化させるモデルとして、ニューラルネットワークを導入した
-
ニューラルネットワークは任意の関数を表現できることがわかった
ニューラルネットワークは非常に多くのパラメータをもつ
(全結合層は、とのパラメータを持つ)
⇨ 学習は、かなりむずかしいタスク
ニューラルネットワーク研究の歴史を遡ってみると...
- 1950年代: パーセプトロン
- 1986年ごろ?: 多層パーセプトロン
→ ニューラルネットで全部表現できる!すごい!!
→ 数学的な研究も進み始める
1990年 ~ 2000年代ごろ
- ニューラルネットワークを大きくしていくと全然学習がうまくいかない
(= まともなパラメータを獲得してくれない)
⇨ ニューラルネットワークはオワコン!
 < :oisu-:
< :oisu-:
ジェフリー・ヒントン(Geoffrey Everest Hinton)

- オートエンコーダによる初期化など、学習を安定化させる方法を提案
⇨ ニューラルネットワークの学習ってがんばればうまくいく?
⇨ 2010年代に入って、ニューラルネットワークが再び注目される
おしながき
- 勾配降下法をニューラルネットワークに適用するための工夫
- ニューラルネットワークを評価する
微分係数
-
微分係数 は、
における接線の傾き⬇︎
方向に関数を少し動かすと、関数の値はすこし小さくなる
勾配降下法
関数 と、初期値 が与えられたとき、
次の式で を更新する
( は学習率と呼ばれる定数)
勾配降下法...
をニューラルネットワークに適用するための色々な技法

⇩

のそれぞれをカスタマイズします
ニューラルネット向けに書き直すとパラメータをならべたベクトルと、の関数である損失関数に対して
と定義される式に沿って更新するという感じになります。
勾配降下法...
はわれわれが決めなければいけなかった!
⇨ どう決めるのがいいのか?
1. Xavierの初期値
2. Heの初期値
Xavierの初期値
2010年、Xavierらが提案
(は全結合層の入力の次元)
おきもち... 活性化関数の微分が「いい感じ」に働く分布になるよう初期値を置く
“Understanding the difficulty of training deep feedforward neural networks" [Glorot and Bengio, 2010]
https://proceedings.mlr.press/v9/glorot10a/glorot10a.pdf
Heの初期値
2015年、Kaiming Heらが提案
-
初期値の決め方は知見が蓄積されている
-
活性化関数などの性質によってこういう初期化がいい、みたいな知見もある
- 例) 活性化関数にを使うSIRENと呼ばれるモデルではがいいなど
-
たいていの場合はフレームワークのデフォルトの初期化方法を使えばいいので、特にいじる場面は多くない(最近は特に必要性が薄れている...正規化層)
-
特殊なネットワークを作るときには、初期化方法をいじるといいかもしれない

⇩

のそれぞれをカスタマイズします
損失関数は
⇨ これを計算するには、回の計算が必要
⇨ データ数が少ない場合はいいが、数GB, TB, ......となっていく
⇨ メモリに乗り切らず実用的な速度で計算することが難しくなる!
 データをランダムにいくつか選んで、そのデータだけを使って損失関数を計算する
データをランダムにいくつか選んで、そのデータだけを使って損失関数を計算する
例) データ数から個のデータをランダムに選ぶ
⇨ メモリに乗り切って計算できる!
この選んだ小さいデータの集合のことをミニバッチと呼び、
そのサイズを バッチサイズ(batch size) と呼ぶ
そしてこれを使った勾配降下法を「確率的勾配降下法」という
確率的勾配降下法を単一データのみの損失を計算して行う手法と呼ぶ派閥もいるみたいですが、ミニバッチ学習に対しても確率的勾配降下法と呼ぶ人が多いと思います。

の、の計算はできるようになった!
Next
⇨ 更新式自体もいじる
局所最適解 ... 付近では最小値だが、全体の最小値ではない
大域最適解 ... 全体で最小値
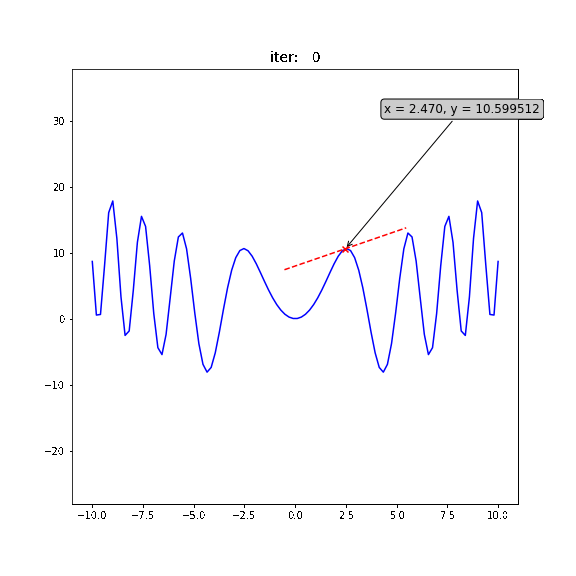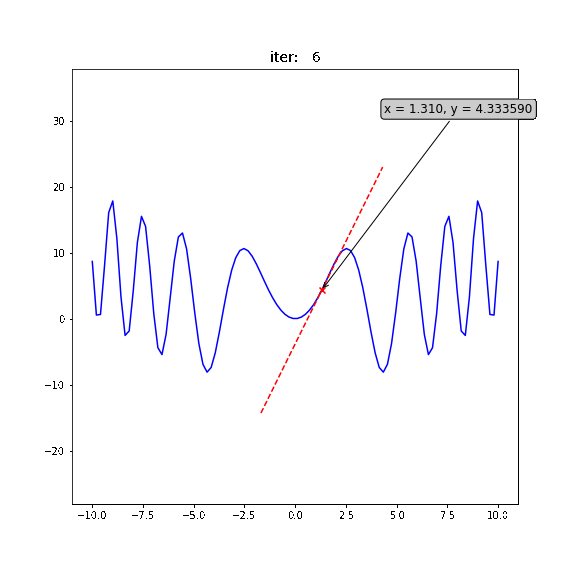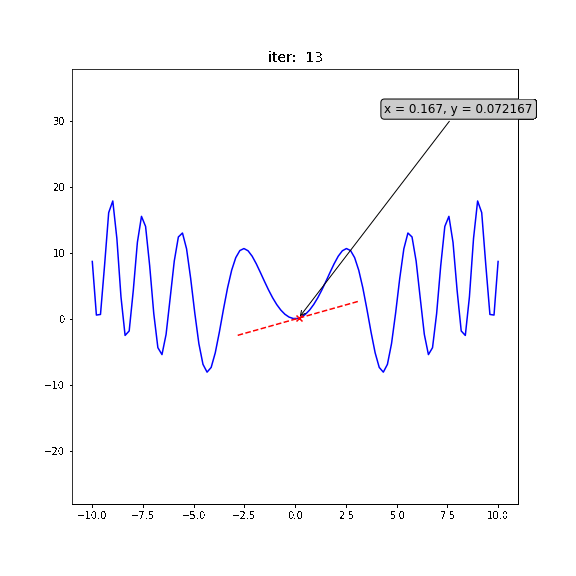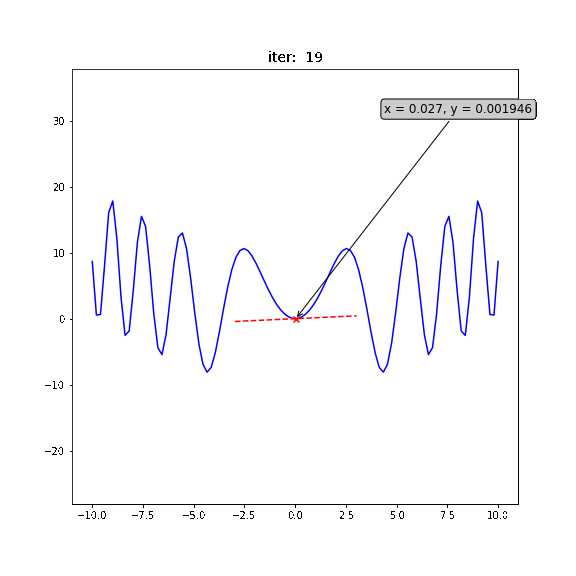
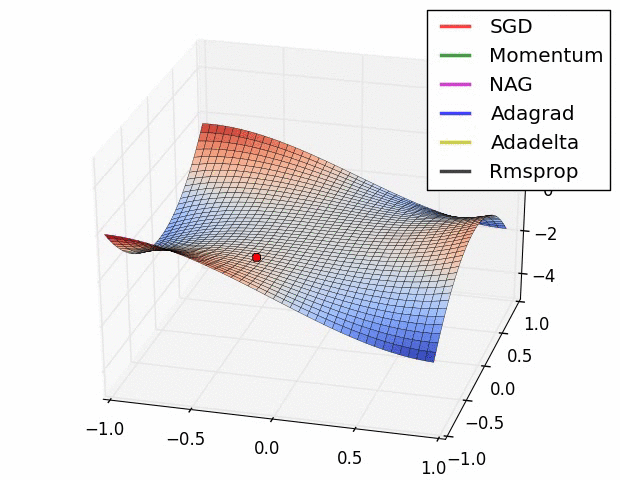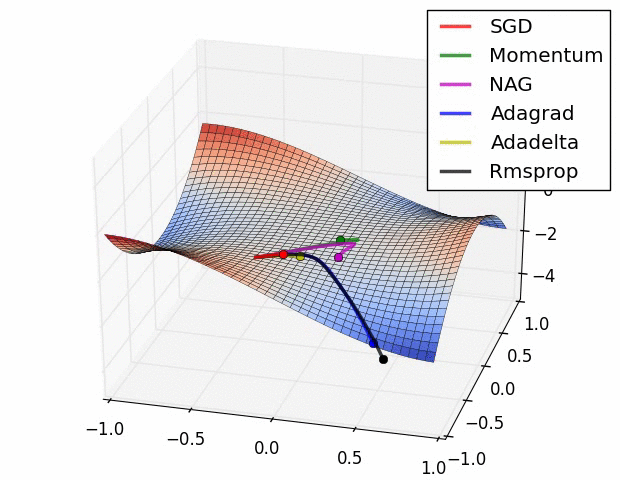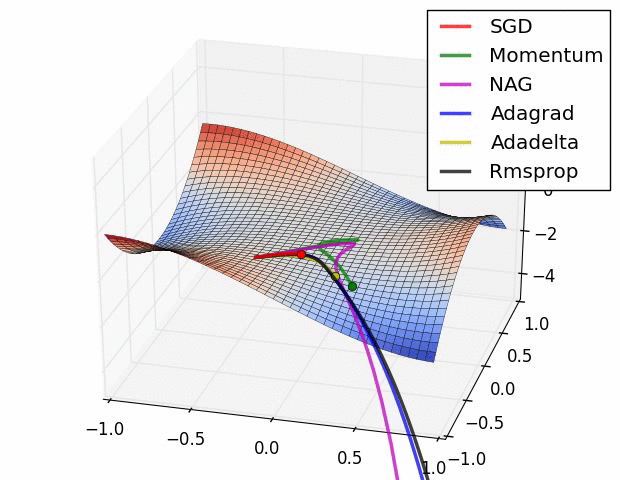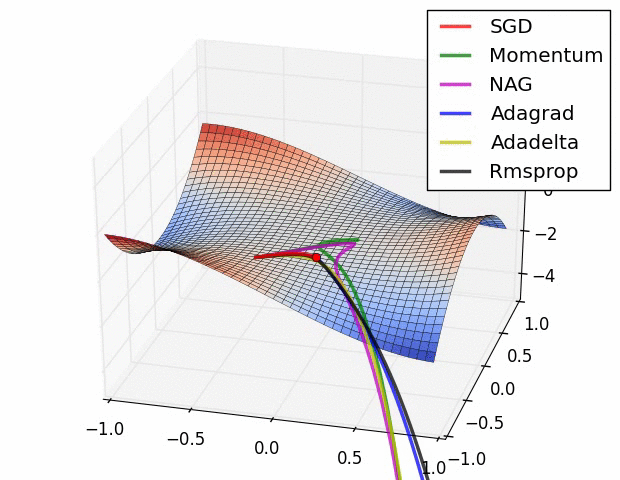
局所最適解にハマりにくい工夫された更新式をもつ色々なオプティマイザが提案されている
他にも学習率()を変化させる手法など、いろいろと工夫されている
⇨ 基本的に、Adam(とその派生系)とSGDが使われることが多い
(使い方は第6回でやります!)

⇩

 「学習」部分は完了
「学習」部分は完了
- 例) アイスの予測ができるモデルが完成した!!!
⇨ こいつの「良さ」をどう定義するべきか
今までは、損失関数の値が小さいほど良いと考えていた(学習時)
⇩
例) アイスの値段予測をするモデルを作った!
学習の際に使ったデータは、
(20℃, 300円), (25℃, 350円), (30℃, 400円), (35℃, 450円), (40℃, 500円)
⇨ さぁこれを使ってアイスの値段を予測するぞ!
⇨ 来るデータは....
(22℃, 24℃, 25℃, ......)
※ 重要: これらの正解データは(少なくとも推論をする段階では)
存在しない
 < なんか来月の予想平均気温30度って気象庁が言ってたな。
< なんか来月の予想平均気温30度って気象庁が言ってたな。
来月の売り上げが予想できたらどのくらい牛乳仕入れたらいいかわかって嬉しいな。
⇨ われわれの全体としての本当の目的はこれらの答えが存在していないデータに対して精度良く推論すること
ところが、まだ答えが存在していないデータを使って学習を行うことはできない!
(なぜなら、答えがないので誤差が定義できない)
⇨ (20℃, 300円), (25℃, 350円), ... ,(40℃, 500円) に対して
妥当な推論が行えるようになったのなら、21℃や26℃に対しても「ある程度」妥当な推論が行えるようになっているはず
このように知らないデータに対しても推定が行えることを汎化といいます。かっこいいですね。この汎化をどのように実現するかと言うのが機械学習の主要な課題です。
学習後に関心があること: 未知のデータへの予測性能
⇨ これを検証しておこう
バリデーション
- 学習データを分割して、一部を学習に使い、残りを検証に使う
学習データ
(20℃, 300円), (25℃, 350円), (30℃, 400円), (35℃, 450円), (40℃, 500円)
-
学習データ
(20℃, 300円), (25℃, 350円), (30℃, 400円) -
検証用データ
(35℃, 450円), (40℃, 500円)
- 学習データ
(20℃, 300円), (25℃, 350円), (30℃, 400円)
のみで学習をおこなう
(35℃, 450円), (40℃, 500円)に対して推論を行い、誤差を評価
400円、500円と推論したとすると、
「検証用データに対する」平均二乗誤差は
- 学習データ
(20℃, 300円), (25℃, 350円), (30℃, 400円)
のみで学習し、検証用データは学習に関与させない
何をしている?
⇨ 擬似的に未知のデータを作成して、
「未知のデータに対する推論の精度」を擬似的に評価している
これらは、学習とは全く独立した作業
⇨ これの計算結果に基づいてモデルが影響を受けることはない
⇩
損失関数が満たす必要があった
- 微分可能
- 微分がほとんど0にならない
などの条件は必要ない!
この検証用データに対して定義される評価の指標を
「評価指標」 という。
\ 重要 / \ 重要 / \ 重要 /
「損失関数」と評価指標は別の概念
\ 重要 / \ 重要 / \ 重要 /
例) アイスの予測では損失関数として平均二乗誤差を使ったが、
別に評価指標が平均百乗乗誤差でもok.
これらは、学習とは全く独立した作業
⇨ これの計算結果に基づいてモデルが影響を受けることはない
⇩
逆にいえば評価指標は直接最適化の対象にはならない!
⇨ うまく設計された損失関数を使って、
評価指標の値を最適化できるように頑張る
つまり...
損失関数の値は、あくまで「訓練データに対してこれくらいの誤差になるよ」という値
⇨ われわれが興味があるのは、知らないデータに対してどれくらいうまく予測できるか
これの検証のために、擬似的に学習に使わない未知のデータを作り、未知のデータに対する予測の評価をする
バリデーションの手法や切り方についてはいろいろあり、話すとかなり長くなりますのでここでは割愛します。メジャーなものだとCross Validationや時系列を意識したValidationなどがあります。
ニューラルネットワークの万能近似性から、(矛盾のないデータからうまく学習さえできれば) 学習時の損失を0にすることができる
⇨ 一方で、検証用データに対しては、損失が大きくなる場合がある
過学習
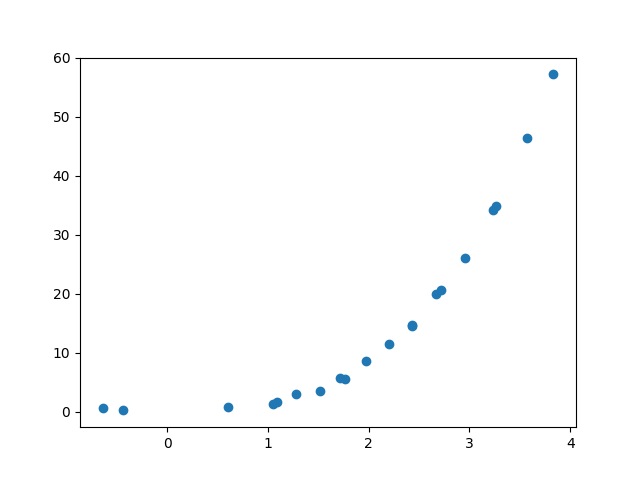
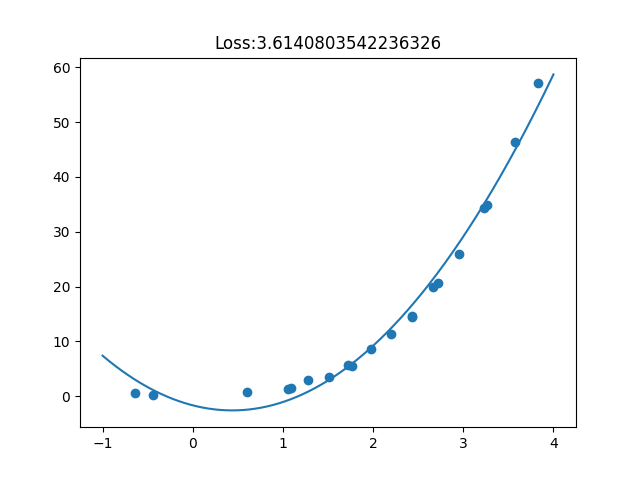
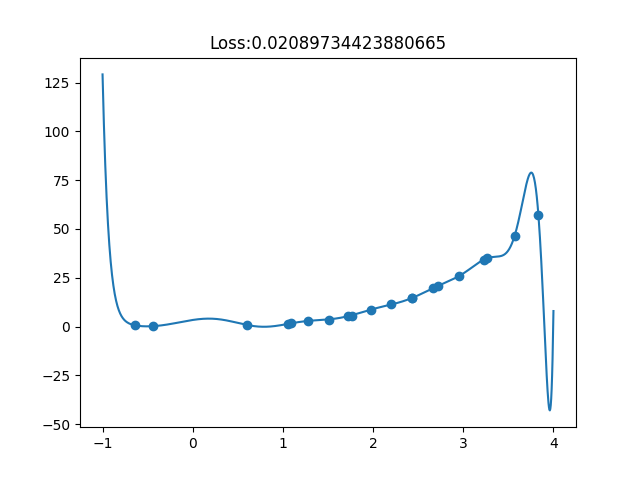
横軸... 学習ステップ
縦軸... 評価(学習時 or バリデーション)
 < 「AI作りました!ちなみにどのくらいの精度で動作するかはわからないです笑」
< 「AI作りました!ちなみにどのくらいの精度で動作するかはわからないです笑」
⇨ きちんとバリデーションを行い、未知のデータに対する予測性能を評価することが大切
⇨ 逆に、適切にバリデーションを行なっていないが故の嘘に気をつけよう!!
~ Learning Curve 閲覧 TIME ~
Kaggleをはじめとするデータ分析コンペは、
「未知の情報」を予測するモデルの精度を競う
⇨ 試行錯誤している手法の、「未知の情報を予測する能力」(=汎化性能)をきちんと評価することが大切!!!!!!!!

 < "A good CV is half of success."
< "A good CV is half of success."
bestfitting
- ニューラルネットワークは、学習において培われてきたいろいろな工夫があった
- バリデーションを行うことで、未知のデータに対しての予測性能「汎化性能」を評価することができる
- バリデーションデータに対して行う評価は、学習とは独立した作業なので、微分可能であったり微分の性質が良い必要はなく、いろいろな評価指標を用いることができる
- 訓練データのみに過剰に適合した状態のことを「過学習」といい、学習曲線に目を光らせるととでこれに気をつける必要があった
機械学習講習会 第六回
- 「ニューラルネットワークの実装」 です!
Jupyter / Google Colaboratoryで今回使う新規ファイルを作成して
構えて待機しておいてください
機械学習講習会 第六回
- 「ニューラルネットワークの実装」
traP アルゴリズム班 Kaggle部
2023/7/3
第一回: 学習
第二回: 勾配降下法
第三回: 自動微分
第四回: ニューラルネットワークの構造
第五回: ニューラルネットワークの学習と評価
第六回: ニューラルネットワークの実装
セルに、以下のコマンドを入力:
!curl -L https://abap34.com/ml-lecture/train.csv -o train.csv
!curl -L https://abap34.com/ml-lecture/test.csv -o test.csv

- train.csv
3211 行 x 17列 - test.csv
803 行 x 16列

 はキッチンカーでアイスを売っています。
はキッチンカーでアイスを売っています。
なるべく多くの売り上げをあげたいので、売り上げを予測する
モデルを構築して、売り上げを予測することにしました。
そこで、ある日に行ったところの気温や降水量などの気象データ、いく地域の人口に占める子供の割合、アイスの値段などなどと、売り上げをまとめたデータを作りました。(train.csv)
そこで、  のために気象データや値段などから、売り上げを予測するモデルを作って、未知のデータ(test.csv)に対して予測してください!
のために気象データや値段などから、売り上げを予測するモデルを作って、未知のデータ(test.csv)に対して予測してください!
https://dacq.trap.show/
予測結果を投稿して、精度を競えます!!!!すごい!!!!

https://dacq.trap.show/
自分のベストスコアを更新すると、激アツアニメーションが見れます!!!!すごいぜ!!!!!!!!!!!!!!!!!!!!!!!!
最高スコアを更新してtraQに投稿しよう!

- データの読み込み
- モデルの構築
- モデルの学習
- 新規データに対する予測
- 順位表への提出
1-1. データの読み込み
⬇︎
1-2. データの前処理
⬇︎
1-2. PyTorchに入力できる形に
# pandasパッケージを`pd`という名前をつけてimport
import pandas as pd
# これによって、pandasの関数を`pd.関数名`という形で使えるようになる
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")

pd.read_csv(path)で、pathにあるcsvファイルを読み込める
パスとは、ファイルの場所を示す文字列のことです。
今回は、train.csvとtest.csvが、ノートブックと同じ場所にあるので、"train.csv"と"test.csv"という文字列をパスとして指定しています。例えば、"/home/abap34/train.csv"というパスを指定すると、"/home/abap34"というフォルダの中にあるtrain.csvというファイルを読み込みます。他にもノートブックの位置からの相対パスを指定することもできます。例えば、"../train.csv"というパスを指定すると、ノートブックの一つ上のフォルダにあるtrain.csvというファイルを読み込みます。
train
とだけセルに入力すると

test
とだけセルに入力すると

今までは...
x = [1, 2, 3, 4, 5]
y = [2, 4, 6, 8, 10]
def loss(a):
n = len(x)
s = 0
for i in range(n):
s += (y[i] - a * x[i])**2
return s / n
⇨ 今回のデータも入力と出力(の目標) に分けておく
train['カラム名']
で「カラム名」という名前の列を取り出せる
⬇︎
今回の予測の目標は
train['売り上げ']
セルに、
train_y = train['売り上げ']
と入力して実行
⇨ train_yに売り上げの列が入る
逆に、モデルに入力するデータは、trainから売り上げの列を除いたもの
train.drop(columns=['カラム名'])
を使うと、trainから「カラム名」という名前の列を除いたものを取り出せる
⬇︎
今回は「売り上げ」を除けば良いので、
train.drop(columns=['売り上げ'])
セルに、
train_x = train.drop(columns=['売り上げ'])
と入力して実行
⇨ train_xに売り上げの列を除いたデータが入る
 データの読み込みが完了!
データの読み込みが完了!
今の状況...
train_x...モデルに入力するデータ(気温、値段、etc...)train_y...モデルの出力の目標(売り上げ)test...予測対象のデータ(気温、値段、etc...)
が入っている

学習の安定性や精度を向上可能
今回は、
各列に対して「標準化」と呼ばれる処理を行う
標準化
(は平均、は標準偏差)
- 平均のデータの全ての要素からを引くと、平均は
- 標準偏差のデータの全ての要素をで割ると、標準偏差は
⇨ 標準化によって、平均を0、標準偏差を1にできる
scikit-learnというライブラリのStandardScalerを使うと、簡単に標準化できる!
# sklearn.preprocessingに定義されているStandardScalerを使う
from sklearn.preprocessing import StandardScaler
# StandardScalerのインスタンスを作成
scaler = StandardScaler()
scaler.fit(train_x)
train_x = scaler.transform(train_x)
test = scaler.transform(test)
scalar.fit関数によって引数で渡されたデータの各列ごとの平均と標準偏差を計算され、scalarに保存されます。そして、scalar.transform関数によってデータが実際に標準化されます。勘がいい人は、「testに対してもtrain_xで学習した平均と標準偏差を使って標準化しているけど大丈夫なのか?」と思ったかもしれないですね。結論から言うとそうなのですが、意図しています。ここに理由を書いたら信じられないくらいはみ出てしまったので、省略します。興味がある人は「Kaggleで勝つデータ分析の技術」p.124あたりを参照してみてください。
train_x
test
などをセルに入力して実行してみると、
確かに何かしらの変換がされている
(ついでに、結果が数字だけになっている)
ので、train_yも数字だけにしておく
train_y = train_y.values.reshape(-1, 1)
最初のテーブルっぽい情報を持ったまま計算を進めたい場合は、
train_x[:] = scaler.transform(train_x)のようにすると良いです.
バリデーションのためにデータを分割しておく

(あんまり前処理には含めない人が多いと思いますが。。。。。。。。ここでやっておきます!)
scikit-learnのtrain_test_splitを使うと、簡単にデータを分割できる!
from sklearn.model_selection import train_test_split
train_x, val_x, train_y, val_y = train_test_split(train_x, train_y, test_size=0.3, random_state=34)
train_test_split(train_x, train_y, test_size=0.3, random_state=34)
- (train_x, train_y)を、学習データ:検証データ = 7:3に分割
train_x.shape
val_x.shape
を確認すると、確かに7:3に分割されていることがわかる

数としてTensor型を使って自動微分などを行える
>>> x = torch.tensor(2.0, requires_grad=True)
>>> def f(x):
... return x ** 2 + 4 * x + 3
...
>>> y = f(x)
>>> y.backward()
>>> x.grad
tensor(8.)
(のにおける微分係数)
⇨ データをTensor型に直しておく
torch.tensor関数によるTensor型のオブジェクトの作成
torch.tensor(data, requires_grad=False)
data: 保持するデータ(配列っぽいものならなんでも)- リスト、タプル、NumPy配列、スカラ、...
requires_grad: 勾配を保持するかどうかのフラグ- デフォルトはFalse
- 勾配計算を行う場合はTrueにする
import torch
train_x = torch.tensor(train_x)
train_y = torch.tensor(train_y)
val_x = torch.tensor(val_x)
val_y = torch.tensor(val_y)
test = torch.tensor(test)
我々が勾配降下法で使うのは、
損失についての各パラメータの勾配
⇨ 入力データに対する勾配は不要なので
requires_grad=True とする必要はない
 1-1. データの読み込み
1-1. データの読み込み
⬇︎
 1-2. データの前処理
1-2. データの前処理
⬇︎
 1-2. PyTorchに入力できる形に
1-2. PyTorchに入力できる形に
- データの読み込み
- モデルの構築
- モデルの学習
- 新規データに対する予測
- 順位表への提出
今からすること...
をつくる
torch.nn.Sequentialによるモデルの構築
入力層は16次元の入力を受け取り、出力が32次元の全結合層
隠れ層は一つあり、32次元の入力を受け取り、出力が64次元の全結合層
出力層は64次元の入力を受け取り、出力が1次元の全結合層
import torch.nn as nn
model = nn.Sequential(
nn.Linear(16, 32),
nn.Sigmoid(),
nn.Linear(32, 64),
nn.Sigmoid(),
nn.Linear(64, 1)
)
import torch.nn as nn
model = nn.Sequential(
nn.Linear(16, 32),
nn.Sigmoid(),
nn.Linear(32, 64),
nn.Sigmoid(),
nn.Linear(64, 1)
)
nn.Sequentialは、順番に層をつなげていくモデルを作るためのクラス
引数に層を順番に渡すことで、モデルを構築してくれる
⇨ すでにこの時点でパラメータの初期化などは終わっている
model.parameters()またはmodel.state_dict()でモデルのパラメータを確認できる
model.state_dict()
を実行すると、モデルが持つパラメータ一覧を確認できる
構築したモデルは、関数のように呼び出すことができる
import torch
dummy_input = torch.rand(1, 16)
model(dummy_input)
torch.randで、ダミーのインプットを作成
⇨ モデルに入力
(現段階では、初期化されて学習されていない重みによる計算)
 をつくる
をつくる
⇨ あとはこれを勾配降下法の枠組みで学習させる!
思い出すシリーズ
確率的勾配降下法
(ミニバッチ学習)
- データの読み込み
- モデルの構築
- モデルの学習
- 新規データに対する予測
- 順位表への提出
3-1. ミニバッチ学習のための準備
⬇︎
3-2. 確率的勾配降下法の実装
ミニバッチ学習
損失関数は
⇨ これを計算するには、回の計算が必要
⇨ データ数が少ない場合はいいが、数GB, TB, ......となっていく
⇨ メモリに乗り切らず実用的な速度で計算することが難しくなる!
 データをランダムにいくつか選んで、そのデータだけを使って損失関数を計算する
データをランダムにいくつか選んで、そのデータだけを使って損失関数を計算する
例) データ数から個のデータをランダムに選ぶ
⇨ メモリに乗り切って計算できる!
この選んだ小さいデータの集合のことをミニバッチと呼び、
そのサイズを バッチサイズ(batch size) と呼ぶ
そしてこれを使った勾配降下法を「確率的勾配降下法」という
確率的勾配降下法を単一データのみの損失を計算して行う手法と呼ぶ派閥もいるみたいですが、ミニバッチ学習に対しても確率的勾配降下法と呼ぶ人が多いと思います。
つまり...
我々がやらなきゃいけないこと
- データをいい感じにランダムに選んで供給する仕組みを作る
...
...
 < 私がやろう
< 私がやろう

torch.utils.data.Datasetとtorch.utils.data.DataLoaderを
使うと、簡単に実装できる!
- 現状確認...
train_x, train_y, val_x, val_y, testをTensor型で保持している
DatasetとDataLoaderの作成
# データセットの作成
train_dataset = TensorDataset(train_x, train_y)
val_dataset = TensorDataset(val_x, val_y)
# データローダの作成
batch_size = 32
train_dataloader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, drop_last=True)
val_dataloader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)
⇩
1. Datasetの作成(Dataset型)
- データセット(データの入出力のペア)を表すオブジェクト
TensorDatasetに
- モデルの入力データ(
train_x)と - 出力の目標データ(
train_y)を渡すことでDataset型のオブジェクトが作られる
実際は
torch.utils.data.Datasetを継承したクラスを作ることでもDataset型(のサブクラス)のオブジェクトを作ることができます。この方法だと非常に柔軟な処理が行えるためこの方法が主流流です。(今回は簡単のためにTensorDatasetを使いました。)
from torch.utils.data import TensorDataset
# データセットの作成
# 学習データのデータセット
train_dataset = TensorDataset(train_x, train_y)
# 検証データのデータセット
val_dataset = TensorDataset(val_x, val_y)
1. DataLoaderの作成(DataLoader型)
Datasetからミニバッチを取り出して供給してくれるオブジェクト
つまり....
- データをいい感じにランダムに選んで供給する仕組みを作る
をやってくれる
1. DataLoaderの作成(DataLoader型)
Datasetからミニバッチを取り出して供給してくれるオブジェクト
DataLoader(dataset, batch_size=batch_size, shuffle=shuffle)
from torch.utils.data import DataLoader
batch_size = 32
train_dataloader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, drop_last=True)
val_dataloader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False)
⇨ これをfor文で回すことでデータを取り出すことができる
1. DataLoaderの作成(DataLoader型)
for inputs, targets in train_dataloader:
print('inputs.shape', inputs.shape)
print('targets.shape', targets.shape)
print('-------------')
⇩
inputs.shape torch.Size([32, 16])
targets.shape torch.Size([32, 1])
-------------
inputs.shape torch.Size([32, 16])
targets.shape torch.Size([32, 1])
...
我々がやらなきゃいけないこと
- データをいい感じにランダムに選んで供給する仕組みを作る
をやってくれる
 完了
完了
 データは回るようになった
データは回るようになった
⇨ あとは学習を実装しよう!
TODOリスト
- 損失関数を設定する
- 勾配の計算を行う
- パラメータの更新を行う
1. 損失関数を設定する
今回は、平均二乗和誤差(Mean Squared Error)を使う
⇨ これもPyTorchには用意されている
criterion = nn.MSELoss()
とすれば、
criterion(torch.tensor([1.0., 2.0, 4.0]), torch.tensor([2.0, 3.0, 4.0]))
と計算してくれる!
TODOリスト

2. 勾配の計算を行う
3. パラメータの更新を行う
2. 勾配の計算を行う
やりかたは....?
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward(), 定義→計算→backw
定義→計算→backward(), 定義→計算→backward() 定義→計算→backw
# ここから
import torch.nn as nn
model = nn.Sequential(
nn.Linear(16, 32),
nn.Sigmoid(),
nn.Linear(32, 64),
nn.Sigmoid(),
nn.Linear(64, 1)
)
# ここまではすでに入力したやつ
dummy_input = torch.rand(1, 16)
dummy_target = torch.rand(1, 1)
# 計算
pred = model(dummy_input)
loss = criterion(pred, dummy_target)
# backward
loss.backward()
チェックポイント
- lossに対する勾配を計算している
# backward
loss.backward()
- 勾配はパラメータに対して計算される
for param in model.parameters():
print(param.grad)
(dummy_input, dummy_targetはrequires_grad=Falseなので勾配は計算されない)
TODOリスト


3. パラメータの更新を行う
for epoch in range(epochs):
for inputs, targets in train_dataloader:
# 計算
outputs = model(inputs)
loss = criterion(outputs, targets)
# backward
loss.backward()
# -----------------------
# ....
# ここにパラメータの更新を書く
# ....
# -----------------------
これまでは、我々が手動(?)で更新するコードを書いていた
⇨  < 私がやろう
< 私がやろう
 torch.optimのオプティマイザを使うことで、簡単にいろいろな最適化アルゴリズムを使える
torch.optimのオプティマイザを使うことで、簡単にいろいろな最適化アルゴリズムを使える
(完成版ではないです!)
optimizer = optim.SGD(model.parameters(), lr=lr)
# 学習ループ
for epoch in range(epochs):
for inputs, targets in train_dataloader:
# 勾配の初期化
optimizer.zero_grad()
# 計算
outputs = model(inputs)
loss = criterion(outputs, targets)
# backward
loss.backward()
# パラメータの更新
optimizer.step()
optimizer = optim.SGD(params, lr=lr)
のようにすることで、paramsを更新の対象とするオプティマイザを作成できる(lrは学習率)
他にも、optim.Adamが使いたければ
optimizer = optim.Adam(params, lr=lr)
とするだけでOK!
⇨ 勾配を計算したあと、optimizer.step()によってパラメータを
更新できる!

optimizer.step()で一回パラメータを更新するたびに
optimizer.zero_grad()で勾配を初期化する必要がある!
(これをしないと前回のbackwardの結果が残っておかしくなる)
⇩ 次のページ...
学習の全体像を貼ります!!!
n_epoch = 10
for epoch in range(n_epoch):
running_loss = 0.0
for inputs, targets in train_dataloader:
# 前の勾配を消す
optimizer.zero_grad()
# 計算
outputs = model(inputs)
loss = criterion(outputs, targets)
# backwardで勾配を計算
loss.backward()
# optimizerを使ってパラメータを更新
optimizer.step()
running_loss += loss.item()
val_loss = 0.0
with torch.no_grad():
for inputs, targets in val_dataloader:
outputs = model(inputs)
loss = criterion(outputs, targets)
val_loss += loss.item()
# エポックごとの損失の表示
train_loss = running_loss / len(train_dataloader)
val_loss = val_loss / len(val_dataloader)
print(f'Epoch {epoch + 1} - Train Loss: {train_loss:.4f} - Val Loss: {val_loss:.10f}')
各行の解説...
- 1行目.
for epoch in range(n_epoch)....n_epoch回分の学習をする - 2行目.
running_loss = 0.0.... 1エポックごとの訓練データの損失を計算するための変数 - 4行目.
for inputs, targets in train_dataloader.... 訓練データを1バッチずつ取り出す(DataLoaderの項を参照してください!) - 6行目.
optimizer.zero_grad().... 勾配を初期化する。二つ前のページのスライドです! - 9, 10行目.
outputs = ....... 損失の計算をします。
-
13行目.
loss.backward().... 勾配の計算です。これによってmodelのパラメータに損失に対する勾配が記録されます -
16行目.
optimizer.step()....optimizerが記録された勾配に基づいてパラメータを更新します。 -
18行目.
running_loss += loss.item().... 1バッチ分の損失をrunning_lossに足しておきます。 -
20行目~25行目. 1エポック分の学習が終わったら、検証データでの損失を計算します。検証用データの内容は、学習に影響させないので勾配を計算する必要がありません。したがって、
torch.no_grad()の中で計算します.
-
28行目〜30行目. 1エポック分の学習が終わったら、訓練データと検証データの損失を表示します。
len(train_dataloader)は訓練データが何個のミニバッチに分割されたかを表す数、len(val_dataloader)は検証データが何個のミニバッチに分割されたかを表す数です。 -
32行目. 損失を出力します。
TODOリスト



+ オプション 学習曲線を書いておこう
- 各エポックの損失を記録する配列を作っておく
train_losses = []
val_losses = []
- 先ほどの学習のコードの中に、損失を記録するコードを追加する
train_loss = running_loss / len(train_dataloader)
val_loss = val_loss / len(val_dataloader)
train_losses.append(train_loss) # これが追加された
val_losses.append(val_loss) # これが追加された
print(f'Epoch {epoch + 1} - Train Loss: {train_loss:.4f} - Val Loss: {val_loss:.10f}')
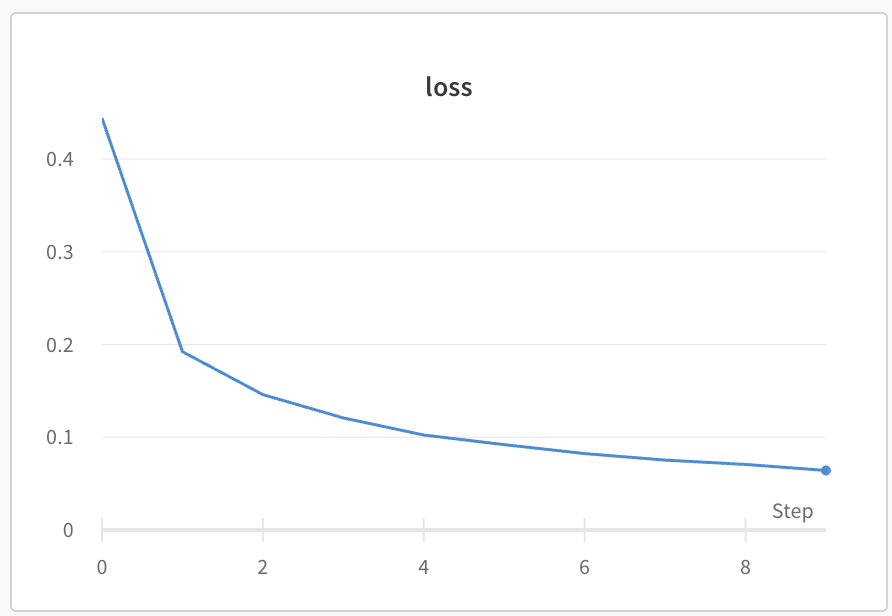
+ オプション 学習曲線を書いておこう
matplotlib というパッケージを使うことでグラフが書ける
# matplotlib.pyplot を pltという名前でimport
import matplotlib.pyplot as plt
plt.plot(train_losses, label='train')
plt.plot(val_losses, label='val')
plt.legend()
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()
⇨ いい感じのプロットを見よう!
- データの読み込み
- モデルの構築
- モデルの学習
- 新規データに対する予測
- 順位表への提出
思い出すシリーズ...
testに予測したい未知のデータが入っている
model(test)
⇨ 予測結果が出る
import csv
def write_pred(predictions, filename='submit.csv'):
pred = predictions.squeeze().tolist()
with open(filename, 'w', newline='') as f:
writer = csv.writer(f)
writer.writerows([[x] for x in pred])
をコピペ
→
write_pred(predictions)を実行すると、submit.csvというファイルが作成されて、予測結果が出力される!! ⇨ これを提出しよう!
https://dacq.trap.show/

めざせ No.1!
できること
- モデルの構造を変えてみる
- オプティマイザーを変えてみる
- 精度が出やすいようにデータを加工する
- 任意に決めた値(
batch_size,lr,n_epochsなど)を変えてみる
次回:
「 ニューラルネットワークの発展」
「 ニューラルネットワークの発展」
- MLP以外のニューラルネットワークのアーキテクチャ
- 最近アツい話
- 今後機械学習を勉強していくにあたって
etc...
部内データ分析コンペを開始します!!!!!!!
- 昨年度も行った部内でのコンペを今年もやります
- 今年は、(ここだけに話) ちょっと豪華になりそうです
- 乞うご期待!!
機械学習講習会 第七回
- 「ニューラルネットワークの発展」
traP アルゴリズム班 Kaggle部
2023/7/4
- 最近あった面白い話
- これまでの振り返り
- ニューラルネットワークの発展
- 今後について
第1回: 学習
第2回: 勾配降下法
第3回: 自動微分とPyTorch
第4回: ニューラルネットワークの構造
第5回: ニューラルネットワークの学習と評価
第6回: ニューラルネットワークの学習
第7回: ニューラルネットワーク発展
モデル
⇩
損失関数
⇩
勾配降下法
⇩
自動微分
⇩
ニューラルネットワーク
- 勾配降下法以外の方法によるパラメータの推定
例: 線形回帰は閉形式解がある
他にも...
...
他のモデル
- サポートベクターマシン
- ランダムフォレスト
- 勾配ブースティング木
などなど...
ニューラルネットワークの発展系
-
畳み込みニューラルネットワーク(CNN)
画像を入力とするネットワークなどで使われる -
Transformer
自然言語処理で使われ始め、近年非常に広い分野で使われる。
広い視野で情報を取れる。とても強い。既存のネットワークをつぎつぎに置き換える性能 -
拡散モデル
ニューラルネットワークを使ってデノイズを繰り返すことで極めて精巧な画像を生成することができる
他のタスクへの応用
今まではアイスの予測を主に扱ってきた
= 実数のベクトルから実数一つへの関数の構築 ()
↓
実際はいろいろなタスクがある
-
教師あり学習
出力の目標が存在していて、それを達成するように学習する- 回帰、分類... etc...
-
教師なし学習
明示的な出力の目標を人間が与えない、クラスタリングなど -
強化学習
環境との相互作用を通して学習する.ゲームAIなど
- 機械学習スタートアップシリーズ
- 機械学習プロフェッショナルシリーズ

- Kaggleで勝つ!データ分析の技術
- ゼロからつくるDeepLearningシリーズ


- Kaggleなどのデータ分析コンペへの参加

実践的な機械学習・データ分析の経験が身につく
日本のコンペプラットフォームもある




- 部内コンペ開催
- 勉強会
- 機械学習講習会(これ)
などなど....
興味がある人はぜひ!
告知:
夏休みに部内コンペを開催します!
ぜひ参加しましょう

